Statistical power is the probability that the test will reject the null hypothesis when the null hypothesis is actually false (i.e. the probability of not committing a Type II error, or making a false negative decision). The probability of a Type II error occurring is referred to as the false negative rate (β). Therefore power is equal to 1 − β, which is also known as the sensitivity.[*]
Increasing the sample size: This is the answer that immediately comes into my mind when talking about increasing the statistical power. It is most likely to detect the effect, if any, when the sample size is increased. 30 is given as the minimum number in many statistical books. I remember "the more is the better" was our approach when conducting research for my master thesis. Increasing sample size has a basic mathematical explanation. When estimating the population mean using an independent and identically distributed (iid) sample of size n, where each data value has variance σ2, the standard error of the sample mean is:
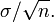
Therefore increasing n will provide a more accurate estimation of the population mean.
Changing the α level: In statistics different α levels are used like 0.5, 0.1 or 0.01. One easy way to increase the power of a test is to carry out a less conservative test by using a larger significance criterion. On the other hand, α levels determine the likelihood of committing a Type I error (declaring a difference that does not exist.) Therefore one should be aware of this risk and evaluate this option accordingly.
Increasing the actual Effect Size: Greater effect size means that there is greater power to detect larger effects. This is not a statistically modifiable condition. However selecting more extreme treatments or experimental conditions might work.
Developing a strong research design: This is about the whole research process. Measurement, sample selection, matching processes should be conducted carefully to ensure the power.
Further analysis: In medicine, for example, tests are often designed in such a way that no false negatives (Type II errors) will be produced. But this inevitably raises the risk of obtaining a false positive (a Type I error). The rationale is that it is better to tell a healthy patient "we may have found something - let's test further," than to tell a diseased patient "all is well."[*]



No comments:
Post a Comment